문제 출처 - Baekjoon Online Judge
문제는 여기
13239번: Combinations
When we have a set of n elements from which we take k elements, we have a combination. For example, if we have a set with the numbers from 1 to 5, we have the following different combinations: 1-combinations (1 element from the set each time): (1), (2), (3
www.acmicpc.net
[문제]
When we have a set of n elements from which we take k elements, we have a combination.
For example, if we have a set with the numbers from 1 to 5, we have the following different combinations:
- 1-combinations (1 element from the set each time): (1), (2), (3), (4), (5)
- 2-combinations (2 elements from the set each time): (1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5).
- 3-combinations (3 elements from the set each time): (1, 2, 3), (1, 2, 4), (1, 2, 5), (1, 3, 4), (1, 3, 5), (1, 4, 5), (2, 3, 4), (2, 3, 5), (2, 4, 5), (3, 4, 5),
- 4-combinations (4 elements from the set each time): (1, 2, 3, 4), (1, 3, 4, 5), (1, 2, 4, 5), (1, 2, 3, 5), (2, 3, 4, 5)
- 5-combination (all the elements at once): (1, 2, 3, 4, 5)
- 0-combination (no element): ()
The following formula will give us the number of k-combinations of n elements:
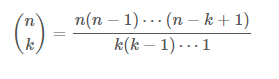
As we saw in the list before
- (5 over 0) = 1
- (5 over 1) = 5
- (5 over 2) = 10
- (5 over 3) = 10
- (5 over 4) = 5
- (5 over 5) = 1
Your task is to compute several (n over k) operations.
[입력]
A line with an integer t. The following t lines will contain 2 integers each separated by spaces. The first value will be n and second k.
- 1 ≤ t ≤ 1000
- 1 ≤ n ≤ 1000
- 0 ≤ k ≤ n
[출력]
For each (n k) pair. Compute the number of k-combinations of a set of size n. Compute the results modulo 1000000007 (10^9 + 7).
[풀이]
1. 값들을 입력받아준다.
2. dp[0][0], dp[1][0], dp[1][1]은 1로 초기화를 해준다.
3. 이후 nCr = n-1Cr-1 + n-1Cr을 이용해 dp 배열을 채워준다.
4. 결과를 출력한다.
[접근]
1. 영어로 되어있지만 막상 보면 nCr에 해당하는 값을 출력해주면 되는 문제다.
2. nCr = n-1Cr-1 + n-1Cr이라는 것을 이용한 dp를 사용해서 문제를 해결하면 되겠다고 생각하였다.
[코드]
import java.io.*;
import java.util.*;
public class Main {
static int mod = 1000000007;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int t = Integer.parseInt(br.readLine());
for (int i = 0; i < t; i++) {
int dp[][] = new int[1001][1001];
StringTokenizer st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
// 초기값을 1로 고정
dp[0][0] = dp[1][0] = dp[1][1] = 1;
// nCr = n-1Cr-1 + n-1Cr 을 이용함
for (int j = 2; j <= a; j++) {
for (int k = 0; k <= b; k++) {
if (j == k || k == 0)
dp[j][k] = 1;
else
dp[j][k] = (dp[j - 1][k - 1] + dp[j - 1][k]) % mod;
}
}
System.out.println(dp[a][b]);
}
}
}'문제 풀이 > Baekjoon' 카테고리의 다른 글
| [백준] G5 17836번 공주님을 구해라! (JAVA) (0) | 2022.07.15 |
|---|---|
| [백준] S1 1743번 음식물 피하기 (JAVA) (0) | 2022.07.14 |
| [백준] G3 2638번 치즈 (JAVA) (0) | 2022.07.12 |
| [백준] S1 1926번 그림 (JAVA) (0) | 2022.07.11 |
| [백준] G3 9466번 텀 프로젝트 (JAVA) (0) | 2022.07.10 |

