문제 출처 - Baekjoon Online Judge
문제는 여기
SW Expert Academy
SW 프로그래밍 역량 강화에 도움이 되는 다양한 학습 컨텐츠를 확인하세요!
swexpertacademy.com
[문제]
우주비행이 꿈이였던 진우는 음식점 '매일매일싱싱'에서 열심히 일한 결과 달 여행에 필요한 자금을 모두 마련하였다! 지구와 우주사이는 N X M 행렬로 나타낼 수 있으며 각 원소의 값은 우주선이 그 공간을 지날 때 소모되는 연료의 양이다.
[예시]
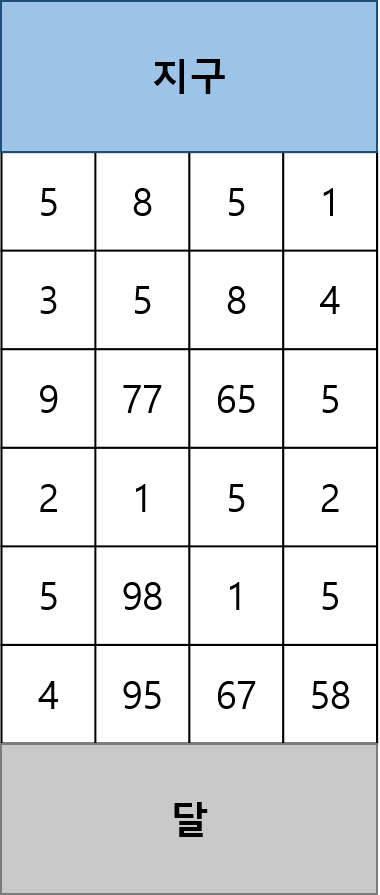
진우는 여행경비를 아끼기 위해 조금 특이한 우주선을 선택하였다. 진우가 선택한 우주선의 특징은 아래와 같다.
1. 지구 -> 달로 가는 경우 우주선이 움직일 수 있는 방향은 아래와 같다.



2. 우주선은 전에 움직인 방향으로 움직일 수 없다. 즉, 같은 방향으로 두번 연속으로 움직일 수 없다.
진우의 목표는 연료를 최대한 아끼며 지구의 어느위치에서든 출발하여 달의 어느위치든 착륙하는 것이다.
최대한 돈을 아끼고 살아서 달에 도착하고 싶은 진우를 위해 달에 도달하기 위해 필요한 연료의 최소값을 계산해 주자.
[입력]
첫줄에 지구와 달 사이 공간을 나타내는 행렬의 크기를 나타내는 N, M (2≤ N, M ≤ 6)이 주어진다.
다음 N줄 동안 각 행렬의 원소 값이 주어진다. 각 행렬의 원소값은 100 이하의 자연수이다.
[출력]
달 여행에 필요한 최소 연료의 값을 출력한다.
[풀이]
1. 값들을 채워준다.
2. 시작지점을 초기화해준다.
3. 올 수 없는 곳에 대해서 max 값으로 초기화해주고 dp 배열을 각 경우에 맞춰서 채워준다.
4. dp 배열의 결과 중 최솟값을 찾아 출력한다.
[접근]
1. 내려가는 방향에 따라서 dp배열을 채워준다.
[코드]
import java.io.*;
import java.util.*;
public class Main {
static int n;
static int m;
static int map[][];
static int dp[][][];
static int max = 999999;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
n = Integer.parseInt(st.nextToken());
m = Integer.parseInt(st.nextToken());
map = new int[n][m];
dp = new int[n][m][3];
// 값 입력받아서 배열 채우기
for (int i = 0; i < n; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 0; j < m; j++) {
map[i][j] = Integer.parseInt(st.nextToken());
}
}
// 출발하는 곳 초기화
for (int i = 0; i < m; i++) {
dp[0][i][0] = map[0][i]; // 왼쪽 대각선
dp[0][i][1] = map[0][i]; // 가운데
dp[0][i][2] = map[0][i]; // 오른쪽 대각선
}
for (int i = 1; i < n; i++) {
// 올 수 없는 곳에 대해서 max 값으로 초기화 해주기
dp[i][0][0] = max;
dp[i][m - 1][2] = max;
for (int j = 0; j < m; j++) {
// 오른쪽에서 못오는 경우
if (!(j - 1 < 0 || j - 1 >= m) && (j + 1 < 0 || j + 1 >= m)) {
dp[i][j][0] = Math.min(dp[i - 1][j - 1][1], dp[i - 1][j - 1][2]) + map[i][j];
dp[i][j][1] = Math.min(dp[i - 1][j][0], dp[i - 1][j][2]) + map[i][j];
}
// 양쪽에서 올 수 있는 경우
else if (!(j - 1 < 0 || j - 1 >= m) && !(j + 1 < 0 || j + 1 >= m)) {
dp[i][j][0] = Math.min(dp[i - 1][j - 1][1], dp[i - 1][j - 1][2]) + map[i][j];
dp[i][j][1] = Math.min(dp[i - 1][j][0], dp[i - 1][j][2]) + map[i][j];
dp[i][j][2] = Math.min(dp[i - 1][j + 1][0], dp[i - 1][j + 1][1]) + map[i][j];
}
// 왼쪽에서 못오는 경우
else if ((j - 1 < 0 || j - 1 >= m) && !(j + 1 < 0 || j + 1 >= m)) {
dp[i][j][1] = Math.min(dp[i - 1][j][0], dp[i - 1][j][2]) + map[i][j];
dp[i][j][2] = Math.min(dp[i - 1][j + 1][0], dp[i - 1][j + 1][1]) + map[i][j];
}
}
}
int min = max;
// 마지막 행에서 최소값 찾기
for (int i = 0; i < m; i++) {
for (int j = 0; j < 3; j++) {
min = Math.min(min, dp[n - 1][i][j]);
}
}
System.out.println(min);
}
}'문제 풀이 > Baekjoon' 카테고리의 다른 글
| [백준] S1 15486번 퇴사 2 (JAVA) (0) | 2022.08.25 |
|---|---|
| [백준] S3 1788번 피보나치 수의 확장 (JAVA) (0) | 2022.08.24 |
| [백준] S1 15645번 내려가기 2 (JAVA) (0) | 2022.08.21 |
| [백준] S4 14495번 피보나치 비스무리한 수열 (JAVA) (0) | 2022.08.20 |
| [백준] S3 25418번 정수 a를 k로 만들기 (JAVA) (0) | 2022.08.15 |


